TLS & Perfect Forward Secrecy
Vincent Bernat
Une fois la clé privée d’un site HTTPS quelconque compromise, un attaquant est capable de monter une attaque par interception (MITM) afin de déchiffrer toutes les communications avec le site compromis. Si l’attaque est détectée, le certificat sera révoqué via une CRL ou un protocole tel que OCSP. Malheureusement, l’attaquant peut aussi avoir en sa position une copie des communications passées de clients avec le serveur. Il est alors capable de déchiffrer celles-ci et y trouver des informations sensibles.
La propriété de forward secrecy1 permet à une information chiffrée aujourd’hui de rester confidentielle en cas de compromission future de la clé privée d’un correspondant. C’est un mécanisme assez coûteux en calculs et de nombreux serveurs font donc l’impasse sur celui-ci. Google a récemment annoncé le support du forward secrecy pour tous ses sites accessibles en HTTPS. Adam Langley a rédigé un article plus détaillé sur ce qui a été réalisé pour améliorer l’efficacité d’un tel mécanisme : avec quelques collègues, il a écrit une implémentation plus efficace pour OpenSSL, basée sur la cryptographie sur les courbes elliptiques.
Mise à jour (08.2019)
Bien que le contenu de cet article soit toujours pertinent, il est important de comprendre qu’il a été rédigé en 2011 et qu’il ne prend pas en compte certains aspects contemporains, notamment la chute de RC4 en tant qu’algorithme approprié et l’omniprésence du forward secrecy dans les déploiements actuels.
Sans forward secrecy#
Pour comprendre ce que le forward secrecy tente de résoudre,
regardons ce qui se passe lors d’une poignée de mains TLS en utilisant
une suite de chiffrement telle que AES128-SHA. Durant celle-ci, le
serveur va présenter son certificat au client et les deux parties vont
s’accorder sur la construction d’un secret maître utilisé par la
suite pour protéger la connexion.

Un premier secret de 48 octets est généré et chiffré par le client avec la clé publique du serveur. Il est envoyé durant la troisième étape de la poignée de mains, lors de l’envoi du message Client Key Exchange. Le secret maître est calculé à partir de celui-ci et des valeurs aléatoires qui ont été transmisses dans les messages Client Hello et Server Hello.
Ce procédé est sûr à condition que seul le serveur puisse déchiffrer le premier secret (à l’aide de sa clé privée) envoyé par le client. Supposons maintenant qu’un attaquant enregistre tous les échanges entre le serveur et ses nombreux clients pendant plusieurs mois. Deux ans plus tard, le serveur est décommissionné et jeté à la benne. L’attaquant en profite pour subtiliser le disque et y trouve la clé privée. Il est désormais capable de déchiffrer toutes les communications qu’il a pu intercepter. Cela lui permet de récupérer, par exemple, des mots de passe encore valides aujourd’hui.
Le problème principal est que la clé privée est à la fois utilisée pour l’authentification du serveur et pour le chiffrement du secret partagé. Alors que l’authentification n’est réellement importante que pendant le laps de temps où la communication entre les deux parties est établie, le chiffrement doit être capable de protéger un secret pendant plusieurs années.
Algorithme de Diffie-Hellman#
Une solution consiste à n’utiliser la clé privée que pour l’authentification et négocier un secret partagé totalement indépendant de celle-ci. Il existe un protocole à cet effet : l’algorithme de Diffie-Hellman. Il s’agit d’une méthode d’échange de clefs ne nécessitant aucune connaissance préalable entre les deux parties. Voici comme cela fonctionne dans le cadre de TLS :
- Le serveur doit initialement disposer de (avec l’aide d’une commande
comme
openssl dhparampar exemple) :, un grand nombre premier, , une racine primitive modulo (pour chaque entier premier avec , il existe un entier tel que ).
- Le serveur choisit un nombre aléatoire
et calcule . Après l’envoi du message Certificate, il envoie un message Server Key Exchange (inclu lors de l’étape 3 mais non représenté dans la poignée de mains décrite précédemment) contenant, en clair mais authentifié avec sa clé privée : - la valeur aléatoire issue du message Client Hello,
- la valeur aléatoire issue du message Server Hello,
, , .
- Le client vérifie la signature et choisit un nombre aléatoire
. Il envoie alors dans un message Client Key Exchange. Il calcule qui constitue le premier secret duquel est dérivé le secret maître. - Le serveur reçoit
et calcule qui est identique au premier secret calculé par le client.
La clé privée n’a été utilisée qu’à des fins d’authentification. Un
espion ne pourra connaître que
Tel que décrit ci-dessus, l’échange de Diffie-Hellman utilise
systématiquement de nouvelles valeurs pour DHE-RSA-AES128-SHA
l’utilisent pour obtenir la propriété de perfect forward
secrecy2.
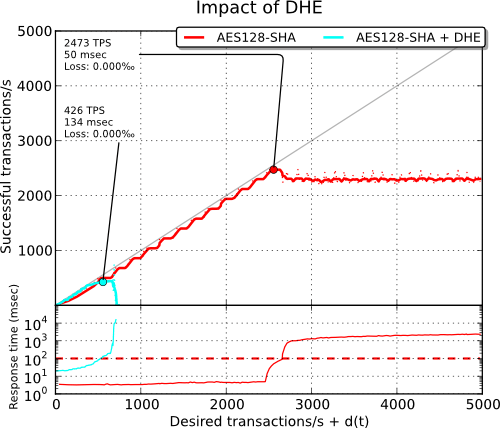
Afin d’obtenir un bon niveau de sécurité, les paramètres utilisés doivent être de la même taille que la clé privée (la sécurité du logarithme discret est environ équivalente à celle fournie par la factorisation de deux grands nombres premiers). Les opérations d’exponentiation sur de tels grands nombres sont alors particulièrement longues et impactent la performance de la poignée de mains comme on peut le voir sur le benchmark ci-dessous :
Mise à jour (05.2015)
L’attaque « Logjam » a démontré que la sécurité de Diffie-Hellman est plus faible que prévue. Notamment, la réutilisation du même nombre premier par de nombreux serveurs permet de précalculer une attaque pour casser les connexions protégées par ce même nombre. Il est donc important que la taille du nombre premier choisi soit équivalente à la taille de la clé RSA (au moins 2048 bits).
Diffie-Hellman et les courbes elliptiques#
L’échange de Diffie-Hellman peut également s’effectuer à l’aide de la cryptographie sur les courbes elliptiques, basée sur la structure des courbes elliptiques sur un corps fini. Pour comprendre comment tout cela fonctionne en détail, l’article de Wikipédia sur les courbes elliptiques est un bon point de départ. Les courbes elliptiques permettent d’obtenir un niveau de sécurité équivalent à RSA en utilisant des clefs plus petites. Par exemple, une courbe elliptique de 224 bits permet d’obtenir un niveau de sécurité similaire à une clé RSA de 2048 bits.
Un peu de théorie#
L’échange de Diffie-Hellman décrit auparavant peut facilement être
adapté pour utiliser les courbes elliptiques. Au lieu d’utiliser deux
entiers
L’utilisation des courbes elliptiques est normalisée comme une extension de TLS et décrite dans la RFC 4492. Contrairement à l’échange de Diffie-Hellman classique, le client et le serveur doivent se mettre d’accord sur les divers paramètres à utiliser. Cet accord se matérialise essentiellement dans les messages Client Hello et Server Hello. Bien qu’il soit possible d’utiliser une courbe elliptique arbitraire, les navigateurs se contentent d’indiquer le support de quelques courbes prédéfinies telles que NIST P-256, P-384 et P-521. L’échange de clefs est ensuite très similaire au cas classique :
- Le serveur choisit un entier aléatoire
et calcule qui sera envoyé en clair, mais signé avec la clé privée du serveur, dans un message Server Key Exchange. - Le client vérifie la signature et choisit un nombre aléatoire
. Il calcule et envoie dans un message Client Key Exchange. Il calcule également qui est le premier secret à partir duquel est calculé le secret maître. - Le serveur reçoit
et calcule . Il peut alors dériver le même secret maître que le client.
Un espion verra passer les valeurs
Utiliser une suite de chiffrement telle que ECDHE-RSA-AES128-SHA
(avec la courbe NIST P-256 par exemple) constitue déjà une
amélioration notable des performances par rapport à la suite
DHE-RSA-AES128-SHA grâce aux nombres plus petits mis en jeu.
Les navigateurs ne supportent qu’une poignée de courbes elliptiques et ces dernières ont été choisies entre autres pour leurs structures facilitant des implémentations efficaces. Le travail effectué par Bodo Möller, Emilia Käsper et Adam Langley consiste à fournir une implémentation optimisée pour les processeurs 64 bits des courbes NIST P-224, P-256 et P-521 pour OpenSSL. Pour obtenir plus de détails sur le sujet, vous pouvez lire la fin de l’introduction aux courbes elliptiques d’Adam Langley puis le court papier d’Emilia Käsper sur l’optimisation de l’implémentation de la courbe NIST P-224.
En pratique#
Tout d’abord, le support des courbes elliptiques n’est pas présent dans tous les navigateurs. Les versions récentes de Firefox et de Chrome supportent les courbes NIST P-256, P-384 et P-521 mais en ce qui concerne Internet Explorer sous Windows XP, il n’y a rien pour le moment. Il faut donc continuer à accepter des suites de chiffrement classiques.
Une version récente d’OpenSSL est nécessaire. Le support pour les
suites ECDHE est apparu dans OpenSSL 1.0.0. Il est simple de
vérifier leur présence avec openssl ciphers ECDH. Pour utiliser la
version optimisée pour 64 bits, il faut se tourner vers la future
version 1.0.1 en la configurant avec l’option
enable-ec_nistp_64_gcc_128. Une version récente de GCC est alors
également requise.
Ensuite, il faut choisir les suites de chiffrement appropriées. Si
le forward secrecy est optionnel, vous pouvez partir sur
ECDHE-RSA-AES128-SHA:AES128-SHA:RC4-SHA qui est compatible avec la
plupart des navigateurs. Si le forward secrecy est obligatoire, il
faudra partir sur quelque chose comme
ECDHE-RSA-AES128-SHA:DHE-RSA-AES128-SHA:EDH-DSS-DES-CBC3-SHA.
Également, il faut s’assurer que l’ordre des suites de chiffrement
est respecté. Pour nginx, il s’agit de la directive
ssl_prefer_server_ciphers on tandis que pour Apache, c’est
SSLHonorCipherOrder on.
Mise à jour (11.2011)
Il est également nécessaire de vérifier que le
support pour ECDHE est présent dans le serveur web que vous
souhaitez utiliser. Pour nginx, le support a été ajouté dans la
version 1.0.6 et dans la version 1.1.0. La courbe elliptique
sélectionnée par défaut est NIST P-256 et il est possible d’en choisir
une autre avec la directive ssl_ecdh_curve. Pour Apache, le
support existe depuis la version 2.3.3 mais n’est pas présent dans la
branche stable. Ajouter le support pour ECDHE n’est pas très
difficile. À titre d’exemple, vous pouvez consulter
comment j’ai ajouté son support dans stud. Le problème est
similaire pour les suites basées sur DHE ; dans ce cas, il peut aussi
être nécessaire de spécifier les paramètres DH à utiliser (générés
avec openssl dhparam) à l’aide de la directive adéquate ou en les
incluant après le certificat. Un
article de Immerda Techblog fournit quelques informations
supplémentaires sur ce point précis.
L’implémentation des tickets de session TLS peut être incompatible avec le forward secrecy selon leur implémentation. Quand la clé protégeant les tickets est générée aléatoirement au démarrage du serveur, la même clé peut être utilisée pendant des mois. Certaintes implémentations 3 optent pour une clé dérivée de la clef privée. Dans ce cas, le forward secrecy est rendu totalement inefficace. Il est alors préférable de désactiver tickets.
La commande openssl s_client -tls1 -cipher ECDH -connect
127.0.0.1:443 permet de vérifier que tout fonctionne comme attendu.
Quelques benchmarks#
En utilisant l’outil de micro-benchmark utilisé lors de mon précédent article, il est possible de comparer l’efficacité de chacune des suites de chiffrement permettant d’obtenir le forward secrecy :
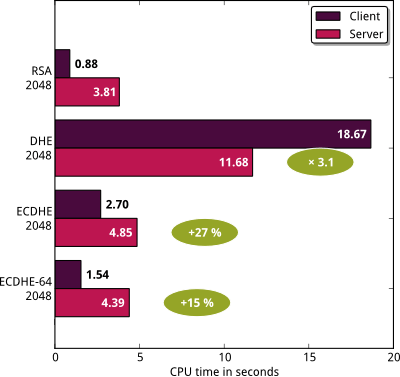
J’ai utilisé une pré-version d’OpenSSL 1.0.1 datant du 25
novembre 2011. La version optimisée d’ECDHE est celle obtenue en
utilisant l’option enable-ec_nistp_64_gcc_128 en configurant
OpenSSL.
Concentrons-nous sur la partie serveur. Activer la suite
DHE-RSA-AES128-SHA grève les performances d’un facteur 3 tandis que
l’utilisation de ECDHE-RSA-AES128-SHA n’implique qu’une pénalité de
27 %. La version optimisée permet de réduire la pénalité à 15 % par
rapport à AES128-SHA. À noter qu’il convient de pondérer de telles
pénalités en fonction du nombre de poignées de mains complètement
effectuées par les clients. Ainsi, si ceux-ci utilisent trois fois sur
quatre une poignée de main raccourcie (reprise d’une ancienne session
TLS), il faut diviser par quatre l’impact sur les performances.
Le coût d’une suite utilisant ECDHE semble donc être plutôt raisonnable par rapport au gain de sécurité apporté. Il s’agit donc d’une option à considérer attentivement lors du choix des suites de chiffrement autorisées.
-
Je ne connais pas la traduction généralement admise pour les termes forward secrecy et perfect forward secrecy. Wikipédia opte pour confidentialité persistante ce qui me semble assez horrible. J’opte donc pour le terme anglais. ↩︎
-
La propriété de perfect forward secrecy est une version améliorée du forward secrecy pour laquelle chaque clé est indépendante l’une de l’autre et la compromission d’une clé ne peut être utilisée pour en compromettre une autre. ↩︎
-
C’est le cas par exemple de l’implémentation que j’ai proposée pour stud afin de permettre le partage des tickets entre plusieurs serveurs. ↩︎